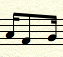How does music improve your math skills?
As you are most likely aware, music is full of math. And although we don’t necessarily teach
musical concepts mathematically, they are nonetheless based in math. Many of these mathematic concepts are taught
through feel. For instance, a dotted
eighth note-sixteenth note pattern might be learned simply as a long-short
The teacher might play the
pattern or clap the pattern after which the student would attempt to copy this
same rhythmic pattern. So the student often
learns to feel various rhythms. But in
learning to feel and play or sing these patterns, one is actually learning to
understand mathematical concepts, some of them rather complex.
Even though we may not teach these musical concepts through
mathematical equations, have you ever thought about how these musical concepts
are expressed in mathematical equations and / or formulas? Well, here are several interesting examples. One must learn to solve many types of
mathematical problems to read music.
Time Signatures:
Time Signatures are actually mathematical expressions. What is 4/4 time? The top 4 tells us there are 4 beats in a
measure. The bottom 4 tells us that each
quarter note gets one beat. Or you
could say there are 4 quarter notes in each measure. A quarter is actually a fractional equivalent
to a fourth (1/4) which is a fraction.
Let’s look at some basic musical stuff. In 4/4 or 3/4 or anything/4, whole notes get 4
beats, half notes get 2 beats and quarter notes get 1 beat.
Addition of whole
numbers:
What if you tie a whole note to a quarter note? You get 5
beats. 4 + 1 = 5. What about a half note tied to another half
note? 2 + 2 = 4. So 2 half notes = 1 whole note.
Subtraction of whole
numbers:
Let’s suppose a measure in 4/4 time has a quarter note on
beat 1. How many beats are left in the
measure, that need to be counted as rests? 4 – 1 = 3.
Multiplication of
whole numbers:
What if the question were asked, “How many beats are there in 8 measures
filled with nothing but whole notes?”
What kind of math is this? Looks
like a multiplication problem: 8 measures x 4 beats = 32 beats.
Division of whole
numbers:
Let’s say we have a piece of music in 4/4 time. There are 36 beats within a given
section. How many measures are in this
section? This could be solved by
dividing 36 beats by 4 beats. 36 ÷ 4
= 9 measures.
So far we’ve done some simple stuff involving basic
operations. But now let’s look at some more complicated things commonly seen in
music.
Order of operations:
Let’s say we’re still in 4/4 time and we encounter a dotted
half note. How do we figure this
out? We know a half note gets 2 beats,
but what is this dot thing? Well, the
dot takes half the value of the note to its left and then adds it onto the
note. So how do you put 2 beats plus
half of 2 beats into equation form? Try
this: 2 + (1/2 * 2) = 3. This problem
involves order of operations (you must solve what’s within the parenthesis
first).
Fractions:
What is an eighth note?
We know we can put 8 eighth notes in 1 measure. But how many beats does it get? We know a whole note gets 4 beats and a half
note gets 2 beats and a quarter note gets 1 beat. It looks like the pattern so far is this: 4 ÷ 2 =
2. 2 ÷ 2 = 1. So, to find the value of an eighth note we
need to divide thus: 1 ÷ 2 =1/2. So an
eighth note gets 1/2 of a beat. But what
about a 16th note? Well, let’s keep the
pattern going. 1/2 ÷ 2 =1/4. So a 16th note gets 1/4 of a beat. This can continue theoretically forever. A 32nd note gets 1/8 of a beat. A 64th note gets 1/16 of a beat and so
on. So now we’re into division involving
fractions.
There’s a lot of fractions in music.
Here’s a few more instances: How
many beats does a dotted quarter note get?
A quarter note gets 1 beat. The
dot after the quarter note adds one-half of the value of the note onto itself. So, as we saw previously, the problem would
go like this: 1 + (1/2 * 1) = 1½.
Adding
fractions using the concepts of equivalent fractions and common denominators:
We can take this dotted note concept further still. How many beats does a dotted eighth note
get? Let’s use the same reasoning and
formula as before. An eighth note gets
1/2 of a beat. If we dot the eighth
note, we have to add one-half the value of the eighth note onto itself so the
equation is 1/2 + (1/2 * 1/2) = what? We
ended up with 1/2 plus 1/4. Now we have
to get a common denominator before we can finish the problem. So we convert 1/2 into 2/4 (these are
equivalent fractions). Then I can add
2/4 + 1/4 and finally get the answer of 3/4.
So now we know that a dotted eighth note gets 3/4 of a beat.
Without going into specifics, the same process has to be followed to
figure out that dotted 16th notes = 3/8 of a beat and dotted 32nd
notes = 3/16 of a beat.
Now things are getting a little more complicated.
Patterns:
Math is full of patterns as is music.
One of the fun things about math is finding these patterns. This is also one of the fun things about
music. Here are some interesting
musical patterns (we’re still thinking in 4/4 time):
Dotted whole note = 6 beats
Dotted half note = 3 beats
Dotted quarter note = 1 ½ beats (which is 3/2 beats)
Dotted eighth note =3/4 of a beat
Dotted sixteenth note = 3/8 of a beat.
Dotted 32nd note = 3/16 of a beat.
Counting
complex passages:
Sometimes, we encounter rather complicated looking musical passages in music. For instance, how do you count this pattern: 16th note-eighth note-16th note. You see this all the time in popular music today. We can think about this a few different ways. We know that a 16th note = 1/4 of a beat. We know that an eighth note = 1/2 or 2/4 or a beat. So these 3 notes make this mathematical equation: 1/4 + 2/4 + 1/4 = 4/4. And as we know 4/4 = 1 whole. So these 3 notes combined make 1 whole beat. One way to count this pattern (so we can figure out how to play it) is to count the quarter beats. In other words, we will divide this 1 beat into 4 parts and count 1-2-3-4 within that 1 beat as is shown to the right.
Let's take an even trickier rhythm. How do play the rhythm shown at the right? How do you count it? Well, we discovered earlier that the 32nd note gets
1/8 of a beat. A dotted 16th gets 3/8 of a beat. So these 4 notes could be represented mathematically as:
3/8 + 1/8 + 3/8 + 1/8 = 8/8 or 1 whole beat. Since the fastest note in this passage is the 32nd note, we'll use it as our basis for subdividing the beat. In other words, we'll divide the beat into 8 parts and count to 8 within that 1 beat. Now there's some fine mathematical figuring.
Tricky stuff (brainteasers):
Math is full of brainteasers. Music has these as well. Here’s one: From C to D is an interval of a
2nd. From D to F is an interval of a 3rd.
So what is it from C to F?
Wouldn’t a 2nd plus a 3rd equal a 5th?
No, that’s not correct. From C to
F is a 4th. Why the apparent
discrepancy?
Here’s another one:
There are 8 notes in a typical scale if you double the starting note (for
example, C Major = C-D-E-F-G-A-B-C).
From C up to F is a 4th.
The inverse of this is F up to the next C, which is a 5th. So, once again, if we add the intervals
together, we get a 9th, but from C to C is only an 8th (most commonly called an
octave).
The answer to our dilemma is: we can’t count the same note
twice. For example, from C to F and from F to C counts the same F twice. If we
only count it once, then things work out nicely.
Metronome markings
and how long each click lasts:
A metronome beats time at different speeds or tempos. If we
set a metronome at 60, it means 60 beats per minute (or 1 beat per
second). This equation would be 60 ÷ 60 = 1 (1
beat per second). So what does a metronome setting of 90 mean? 90 beats per minute, but how many beats per
second is that? 60 ÷ 90 = 2/3
beats per second. That’s not really
something we need to know, but it’s still interesting to know.
The
overtone series, frequencies and algebra:
The overtone series is fascinating and full of mathematical material. Here is a simple explanation of overtones: when a string
is plucked or struck the movement of the string causes a fundamental sound plus
many higher frequencies as well called overtones. The lowest normal frequency is called the
fundamental or first partial. The higher
tones are called overtones. These overtones
are also called partials. Overtones are
multiples of the frequency of the fundamental.
For example, if the fundamental is C at 64 vibrations per second, the
second partial is the octave, at 128 vps (vibrations per second), the third
partial is G at 192 vps, the 4th partial is the next higher C at 256
vps, etc. Thus, an algebraic formula can
be used to find the frequency of the partials.
In this algebraic formula, f stands for frequency, P
stands for the frequency of the partial.
Here’s the formula for the second partial: f x 2 = P
(in this example f is 64). 64 x 2 =
128. f x 3 for the 3rd partial
(64 x 3 = 192), etc. So what would the
frequency be of the 10th partial? Using
our formula, 64 x 10 = 640.
Ratios and the
overtone series:
In order to illustrate this better, let’s look at the first
sixteen partials beginning on a low C.
1) C2 (the 2nd lowest C on the piano).
2) C3 (an octave higher)
3) G3 (up a Perfect 5th)
4) C4 (middle C, up a Perfect 4th and an octave
higher than partial #2)
5) E4 (up a Major 3rd)
6) G4 (up a minor 3rd)
7) Bb4 (up a minor 3rd)
8) C5 (up a Major 2nd and also up another octave
from partial #4)
9) D5 (up a Major 2nd)
10) E5 (up a Major 2nd)
11) F#5 (up a Major 2nd)
12) G5 (up a minor 2nd)
13) A5 (up a Major 2nd)
14) Bb5 (up a minor 2nd)
15) B5 (up a minor 2nd)
16) C6 (up another minor 2nd and up another
octave from partial #8)
An interval may be expressed as a ratio between two
frequencies. For instance, an octave is
a ratio of 1 to 2 (1:2) because we’re comparing Partial 1 (the fundamental or
lowest note) with partial 2. Partials 2
and 3 can be expressed in ratio form as 2:3.
From partial 2 to partial 3 is a Perfect 5th, so a Perfect 5th
can be expressed as the ratio 2:3. What
is the ratio of a Perfect 4th then?
Since it’s a Perfect 4th between partials 3 and 4, then the
ratio is 3:4. What about the ratio
between partials 8 and 16? Partial 8 is
C5 and partial 16 is C6. This is an
octave. The ratio of 8:16 can be reduced
to 1:2, which is the ratio of an octave as we saw earlier.
So, you can see that even the sounds we listen to can be
understood more clearly through the use of math.
When we learn music, we don't usually write out mathematical equations every time we see a dotted note or every time we see a complicated rhythm, but the fact is we are doing math and learning these math skills when we learn music. We start to memorize the patterns and the rhythmic values. These become a part of us and a part of the way we think about things, musically and otherwise.
It is no wonder, then, that those who learn music generally do better in math.
